(I)从正方体的8个顶点中任意取3个构成三角形的顶点共有
其中X=
∴P(X=
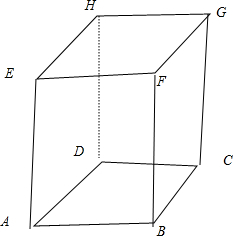 (II)由(I)知,形如△BEG的三角形有8个,其面积为
形如△ABC的三角形有4×6=24个,这些三角形的面积都是
形如△ABG的三角形有4×6=24个,这些三角形的面积都是
而X可能取值有
P(X=
P(X=
∴随机变量X的分布列为 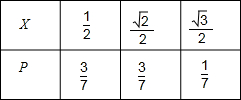 EX=
|
(I)从正方体的8个顶点中任意取3个构成三角形的顶点共有
其中X=
∴P(X=
 (II)由(I)知,形如△BEG的三角形有8个,其面积为
形如△ABC的三角形有4×6=24个,这些三角形的面积都是
形如△ABG的三角形有4×6=24个,这些三角形的面积都是
而X可能取值有
P(X=
P(X=
∴随机变量X的分布列为  EX=
|
题目简介
已知正方体ABCD、EFGH的棱长为1,现从8个顶点中随机取3个点构成三角形,设随机变量X表示取出的三角形的面积.(I)求概率P(X=12);(II)求X的分布形列及数学期望E(X).-数学
题目详情
(I)求概率P(X=
(II)求X的分布形列及数学期望E(X).