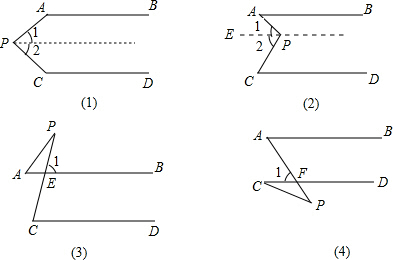如图，AB∥CD，分别探索下列四个图形中∠P、∠A、∠C，发现有如下三种数量关系：∠A+∠C=∠P；∠P+∠A=∠C；∠P+∠C=∠A，请你选择其中的两种数量关系说明理由．（1）我选择的是图_____

题目简介

题目详情

如图，AB∥CD，分别探索下列四个图形中∠P、∠A、∠C，发现有如下三种数量关系：
∠A+∠C=∠P；∠P+∠A=∠C；∠P+∠C=∠A，请你选择其中的两种数量关系说明理由．
（1）我选择的是图______，数量关系式是______理由：
（2）我选择的是图______，数量关系式是______理由：
360优课网

题型：解答题难度：中档来源：不详

答案

（1）∠A+∠P+∠C=360°．
理由：过点P作PE∥AB，
∵AB∥CD，
∴AB∥PE∥CD，
∴∠A+∠1=180°，∠2+∠C=180°，
∴∠A+∠C+∠APC=∠A+∠1+∠2+∠C=360°．

（2）∠P=∠A+∠C．
理由：过点P作PE∥AB，
∵AB∥CD，
∴AB∥PE∥CD，
∴∠1=∠A，∠2=∠C，
∴∠APC=∠1+∠2=∠A+∠C．

（3）∠C=∠A+∠P．
理由：∵AB∥CD，
∴∠1=∠C，
∵∠1=∠A+∠P，
∴∠C=∠A+∠P；

（4）∠A=∠C+∠P．
理由：∵AB∥CD，
∴∠1=∠A，
∵∠1=∠C+∠P，
∴∠A=∠C+∠P．

上一篇 : 如图，AB∥CD∥EF，那么∠BAC+∠AC
下一篇 : 一个宽度相等纸条，按如图所示的

如图，AB∥CD，分别探索下列四个图形中∠P、∠A、∠C，发现有如下三种数量关系：∠A+∠C=∠P；∠P+∠A=∠C；∠P+∠C=∠A，请你选择其中的两种数量关系说明理由．（1）我选择的是图_____

题目简介

题目详情

答案

更多内容推荐