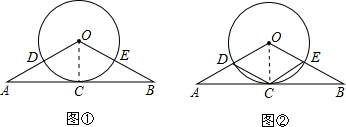
 (1)相切; 理由如下:如图①,连接OC. ∵OA=OB,点C是线段AB的中点, ∴OC⊥AB; 又∵OC是⊙O的半径,点C在⊙O上, ∴直线AB与⊙O相切; (2)如图②,连接OC,则OC=OD; ∵四边形ODCE为菱形, ∴OD=CD, ∴OC=OD=CD, ∴△ODC为等边三角形, ∴∠AOC=60°. 由(1)知,∠OCA=90°, ∴∠A=30°(或∠B=30°或∠AOB=120°). |
 (1)相切; 理由如下:如图①,连接OC. ∵OA=OB,点C是线段AB的中点, ∴OC⊥AB; 又∵OC是⊙O的半径,点C在⊙O上, ∴直线AB与⊙O相切; (2)如图②,连接OC,则OC=OD; ∵四边形ODCE为菱形, ∴OD=CD, ∴OC=OD=CD, ∴△ODC为等边三角形, ∴∠AOC=60°. 由(1)知,∠OCA=90°, ∴∠A=30°(或∠B=30°或∠AOB=120°). |
题目简介
已知,如图,△OAB中,OA=OB,⊙O经过AB的中点C,且与OA、OB分别交于点D、E.(1)如图①,判断直线AB与⊙O的位置关系并说明理由;(2)如图②,连接CD、CE,当△OAB满足什么条件时,
题目详情
(1)如图①,判断直线AB与⊙O的位置关系并说明理由;
(2)如图②,连接CD、CE,当△OAB满足什么条件时,四边形ODCE为菱形,并证明你的结论.