| (1)证明:∵四边形ABEF是矩形, ∴AF=BE,AB=EF,∠BAF=∠ABE=∠AFE=∠BEF=90°. 又∵AB=10,AF=20, ∴AF=2AB, ∵C、D分别是BE、AF的中点, 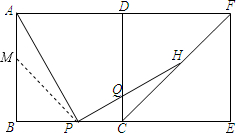 ∴四边形ABCD、CDFE是全等的正方形, ∴∠PCD=90°, ∴∠B=∠PCD,∠QPC+∠PQC=90°, ∵AP⊥PQ, ∴∠APB+∠QPC=90°, ∴∠APB=∠PQC, ∴△ABP∽△PQC; (2)证明:在AB上截取AM=PC, ∵四边形ABCD、CDFE是全等的正方形, ∴AB=BC,∠ECF=45°, ∴BM=BP,∠PCH=135°, ∴∠BMP=45°, ∴∠AMP=135°, ∴∠AMP=∠PCH, ∵△ABP∽△PQC, ∴∠BAP=∠QPC, ∵在△AMP和△PCH中,
∴△AMP≌△PCH(ASA), ∴AP=PH; 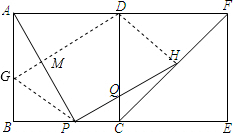 (3)满足条件的点G是存在的,此时AG=BP. 证明如下:令DG与AP的交点为M. ∵四边形ABCD是正方形, ∴DA=AB,∠DAG=∠ABP, ∵在△DAG和△ABP中,
∴△DAG≌△ABP(SAS), ∴DG=AP,∠AGD=∠BPA. ∵AP=PH,∠BAP+∠BPA=90°, ∴DG=HP,∠BAP+∠AGD=90°, ∴∠AMG=90°, 即AP⊥DG, ∵AP⊥PH, ∴DG∥PH, ∴四边形GPHD是平行四边形. |
题目简介
如图,在矩形ABEF中,C、D分别是边BE、AF的中点,AB=10,AF=20,点P、Q分别是BC、CD边上的点,且AP⊥PQ.(1)证明:△ABP∽△PQC;(2)延长PQ交CF于H,求证:AP=P
题目详情
(1)证明:△ABP∽△PQC;
(2)延长PQ交CF于H,求证:AP=PH
(3)在边AB上是否存在一点G,使四边形GPHD是平行四边形?若存在,请给予证明;若不存在,请说明理由.