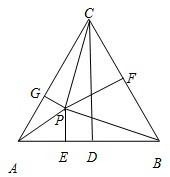
 由于等边△ABC的边长为a,P是△ABC内的任意一点,且P到三边AB,BC,CA的距离分别为d1,d2,d3,则有d1+d2+d3为定值
证明如下:如图,△ABC是等边三角形,点P是等边三角形内部任一点. S△APB=
于是S△APB+S△CPB+S△APC=
即
PE+PF+PG=
即d1+d2+d3=
由线类比为面,点到直线的距离类比为点到平面的距离,面积类比为体积得到: 有d1+d2+d3+d4为定值
故答案为:
|
 由于等边△ABC的边长为a,P是△ABC内的任意一点,且P到三边AB,BC,CA的距离分别为d1,d2,d3,则有d1+d2+d3为定值
证明如下:如图,△ABC是等边三角形,点P是等边三角形内部任一点. S△APB=
于是S△APB+S△CPB+S△APC=
即
PE+PF+PG=
即d1+d2+d3=
由线类比为面,点到直线的距离类比为点到平面的距离,面积类比为体积得到: 有d1+d2+d3+d4为定值
故答案为:
|
题目简介
设等边△ABC的边长为a,P是△ABC内任意一点,且P到三边AB、BC、CA的距离分别为d1、d2、d3,则有d1+d2+d3为定值32a;由以上平面图形的特性类比到空间图形:设正四面体ABCD的棱长
题目详情