| (1)证明:连接EC,FC. ∵AC⊥l1, ∴∠B=∠COE=90°. 在Rt△BCE和Rt△OCE中 又∵BC=CO=a,EC=EC, ∴△BCE≌△OCE(HL). ∴BE=EO.同理OF=FD. ∴AE+AF+EF=AB+AD=2a. (2)如图4,过C作CM⊥EF于M, 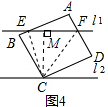 则∠B=∠EMC=90°. 在Rt△BCE和Rt△MCE中, ∵BC=CM=a,EC=EC, ∴△BCE≌△MCE(HL), 同理△CMF≌△CDF 得BE=ME,MF=DF. ∴AE+AF+EF=AB+AD=2a. (3)m1+m2=2a 证明:如图5将l1,l2分别同时向下平移相同的距离,则l4和l3的距离还是a,使得l4经过点C,l3交AB于M,交AD于N 由(2)的证明知AM+MN+AN=2a, 过F作FK∥AB交MN于K. ∴四边形EMKF为平行四边形. ∴EF=MK,FK=EM, ∵作FQ⊥MN于Q,CP⊥GH于P.则FQ=CP. 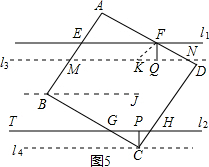 ∵FK∥AB, ∴∠FKQ=∠AMN. 作BJ∥MN, ∴∠AMN=∠ABJ. ∵∠ABJ+∠CBJ=90°,∠CBJ=∠BGT=∠CGP,∠CGP+∠GHC=90°. ∴∠FKQ=∠GHC. ∴△FQK≌△CPH ∴FK=CH,KQ=PH. 同理FN=GC,NQ=GP. ∴KN=GH.则AE+AF+EF+GC+CH+GH, =AE+EM+AF+FN+MK+KN, =AM+AN+MN, =2a. |
题目简介
平面内两条直线l1∥l2,它们之间的距离等于a.一块正方形纸板ABCD的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.(1)如图1,将点C放置在直线l2上,且AC⊥l1于O,使得直-数学
题目详情
(1)如图1,将点C放置在直线l2上,且AC⊥l1于O,使得直线l1与AB、AD相交于E、F,证明:△AEF的周长等于2a;
请你继续完成下面的探索:
(2)如图2,若绕点C转动正方形硬纸板ABCD,使得直线l1与AB、AD相交于E、F,试问△AEF的周长等于2a还成立吗?并证明你的结论;
(3)如图3,将正方形硬纸片ABCD任意放置,使得直线l1与AB、AD相交于E、F,直线l2与BC、CD相交于G,H,设△AEF的周长为m1,△CGH的周长为m2,试问m1,m2和a之间存在着什么关系?试证明你的结论.