如图：已知MN∥PQ，同旁内角的平分线AB、CD和AD、CD分别相交于点．（1）猜想AC和BD间的关系是什么？（2）试用理由说明你的猜想．（本题将按正确结论的难易程度给分）-数学

题目简介

如图：已知MN∥PQ，同旁内角的平分线AB、CD和AD、CD分别相交于点．
（1）猜想AC和BD间的关系是什么？
（2）试用理由说明你的猜想．（本题将按正确结论的难易程度给分） 360优课网

题型：解答题难度：中档来源：不详

（1）答：AC与BD互相平分，且AC=BD，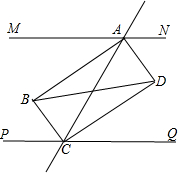

360优课网

（2）证明：∵MN∥PQ，
∴∠MAC=∠ACQ、∠ACP=∠NAC，
∵AB、CD分别平分∠MAC和∠ACQ，
∴∠BAC=class="stub"1

∠MAC、∠DCA=class="stub"1

∠ACQ，
又∵∠MAC=∠ACQ，∴∠BAC=∠DCA，
∴AB∥CD，
∵AD、CB分别平分∠ACP和∠NAC，
∴∠BCA=class="stub"1

∠ACP、∠DAC=class="stub"1

∠NAC，

又∵∠ACP=∠NAC，
∴∠BCA=∠DAC，
∴AD∥CB，
又∵AB∥CD，
∴四边形ABCD平行四边形，
∵∠BAC=class="stub"1

∠MAC，∠ACB=class="stub"1

∠ACP，
又∵∠MAC+∠ACP=180°，
∴∠BAC+∠ACP=90°，
∴∠ABC=90°，
∴平行四边形ABCD是矩形．