 (1)证法1:如图2,延长BC到D,过点C画CE∥BA ∵BA∥CE(作图所知) ∴∠B=∠1(两直线平行,同位角相等), ∠A=∠2(两直线平行,内错角相等). 又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义) ∴∠A+∠B+∠ACB=180°(等量代换). 故答案为:∠1;两直线平行,内错角相等; (2)证法2:如图3,过线段BC上任一点F(点B、C除外),画FH∥AC,FG∥AB, ∴∠1=∠B,∠3=∠C,∠4=∠A, ∵FG∥AB, ∴∠2=∠4, ∴∠2=∠A, ∵∠1+∠2+∠3=180°, ∴∠A+∠B+∠C=180°. |
题目简介
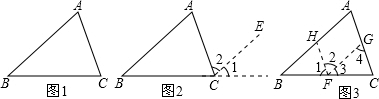
如图1,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一个平角,依辅助线不同而得多种证法.证法1:如图2,延长BC到D,过点-数学
题目详情
分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一个平角,依辅助线不同而得多种证法.
证法1:如图2,延长BC到D,过点C画CE∥BA
∵BA∥CE(作图所知)
∴∠B=______(两直线平行,同位角相等),
∠A=∠2 (______ ).
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义)
∴∠A+∠B+∠ACB=180°(等量代换)
(1)请补全上述证明过程.
(2)如图3,过线段BC上任一点F(点B、C除外),画FH∥AC,FG∥AB,这种添加辅助线的方法也能证明∠A+∠B+∠C=180°.请完成说理过程.
证法2:如图3,过线段BC上任一点F(点B、C除外),画FH∥AC,FG∥AB.