(1)证明:连接OA,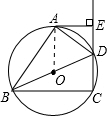 ∵DA平分∠BDE, ∴∠BDA=∠EDA. ∵OA=OD, ∴∠ODA=∠OAD, ∴∠OAD=∠EDA, ∴OA∥CE.(3分) ∵AE⊥DE, ∴∠AED=90°. ∴∠OAE=∠DEA=90°. ∴AE⊥OA. ∴AE是⊙O的切线.(5分) (2)∵BD是直径, ∴∠BCD=∠BAD=90°. ∵∠DBC=30°,∠BDC=60°, ∴∠BDE=120°.(6分) ∵DA平分∠BDE, ∴∠BDA=∠EDA=60°. ∴∠ABD=∠EAD=30°.(8分) ∵在Rt△AED中,∠AED=90°,∠EAD=30°, ∴AD=2DE. ∵在Rt△ABD中,∠BAD=90°,∠ABD=30°, ∴BD=2AD=4DE. ∵DE的长是1cm, ∴BD的长是4cm.(10分) |
题目简介
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若∠DBC=30°,DE=1cm,求BD的长.-数学
题目详情
(1)求证:AE是⊙O的切线;
(2)若∠DBC=30°,DE=1cm,求BD的长.