首页 > 已知：平行四边形ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．（1）求证：四边形ABCD是矩形

已知：平行四边形ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．（1）求证：四边形ABCD是矩形

题目简介

已知：平行四边形ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．（1）求证：四边形ABCD是矩形

题目详情

已知：平行四边形ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿
360优课网
DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．
（1）求证：四边形ABCD是矩形；
（2）在四边形ABCD中，求
AB
BC
的值．
题型：解答题难度：中档来源：淮安

答案


360优课网
（1）证明：连接OE，
∵四边形ABCD是平行四边形，
∴DO=OB，
∵四边形DEBF是菱形，
∴DE=BE，
∴EO⊥BD，
∴∠DOE=90°，
即∠DAE=90°，
又四边形ABCD是平行四边形，
∴四边形ABCD是矩形．

（2）∵四边形DEBF是菱形，
∴∠FDB=∠EDB，
又由题意知∠EDB=∠EDA，
由（1）知四边形ABCD是矩形，
∴∠ADF=90°，即∠FDB+∠EDB+∠ADE=90°，
则∠ADB=60°，
∴在Rt△ADB中，有AD：AB=1：
3
，
又BC=AD，
则class="stub"AB
BC
=
3
．
说明：其他解法酌情给分

更多内容推荐

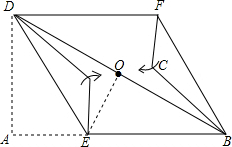
Copyright © 2018-2020 360优课网