如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部分，但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分？用实验或说理的方法，给予探索并得出结论．-数学

题目简介

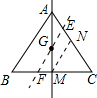
如图，等边△ABC，G是△ABC的重心，直线AG把△ABC分成面积相等的两部分，但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分？用实验或说理的方法，给予探索并得出结论． 360优课网

题型：解答题难度：中档来源：不详

不是．
理由：如图，过G作直线EF∥AB，交AC于E、BC于F，
设直线AG与BC的交点为M，过M作MN∥EF，交AC于N．
∵G是△ABC的内心，
∴BM=MC，AG=2GM．
∵GE∥MN，
∴class="stub"AE

=class="stub"AG

=class="stub"2

，即AE=class="stub"2

AN．
∵BM=MC，即M是BC的中点，且MN∥EF∥AB，
∴MN是△ABC的中位线，即AN=NC．
∴AE=class="stub"2

AN=class="stub"2

NC．
设AE=2x，则AN=NC=3x，EN=x，
∴EC=NC+EN=4x，AC=AE+EC=6x．
∵EF∥AB，
∴△CMN∽△CBA，
∴

S△CMN

S△CBA

=（class="stub"EC

）2=class="stub"4

，
故S△CEF：S四边形AEFB=4：5．
因此过G点的任意一条直线不是都能把△ABC分成面积相等的两部分．