| (1)∵∠A=∠DCB, ∴∠EAC=∠O2CB, 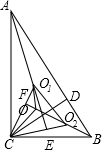 ∴∠EAC+∠ACE=∠O2CB+∠ACE=90°, 即∠AEC=90°, ∴O1O⊥CO2; (2)由于点O1O2分别在∠ACD和∠DCB的平分线上, ∴∠O1CO2=45°,由(1)∠O1EC=90°, ∴CE=O1E, 同理可证O2F⊥CF,∠OO2E=45°,O2E=EO,∠CEO=∠O2EO1, ∴△CEO≌△O1EO2, ∴CO=O1O2. |
| (1)∵∠A=∠DCB, ∴∠EAC=∠O2CB,  ∴∠EAC+∠ACE=∠O2CB+∠ACE=90°, 即∠AEC=90°, ∴O1O⊥CO2; (2)由于点O1O2分别在∠ACD和∠DCB的平分线上, ∴∠O1CO2=45°,由(1)∠O1EC=90°, ∴CE=O1E, 同理可证O2F⊥CF,∠OO2E=45°,O2E=EO,∠CEO=∠O2EO1, ∴△CEO≌△O1EO2, ∴CO=O1O2. |
题目简介
如图,已知Rt△ABC中,CD是斜边AB上的高,O、O1、O2分别是△ABC,△ACD、△BCD的角平分线的交点,求证:(1)O1O⊥CO2;(2)OC=O1O2.-数学
题目详情
求证:(1)O1O⊥CO2;(2)OC=O1O2.