| (1)连接OD; ∵OE∥AB, ∴∠EOC=∠A, 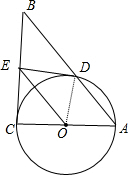 ∵OD=OA, ∴∠ODA=∠A, ∵∠EOC+∠DOE=∠DOC=∠ODA+∠A=2∠A, ∴∠DOE=∠A, ∴∠EOC=∠DOE, 在△OCE和△ODE中,
∴△OCE≌△ODE(SAS), ∴∠C=∠ODE=90°, ∴ED是⊙O的切线; (2)∵OE∥AB,CO=OA, ∴CE=EB; ∴OE是△ABC的中位线; ∴AB=2OE; 在Rt△ODE中, ∵∠ODE=90°,OD=
∴OE=
∴AB=5. 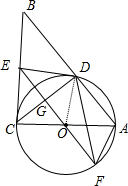 (3)设EF与CD交于点G,DG是Rt△ODE斜边OE上的高; ∴DG=
∴CD=2DG=
Rt△ACD中,∠ADO=90°,AC=3,CD=
∴AD=
∴S△ADF=S△ADG=
|
题目简介
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.(1)求证:ED是⊙O的切线;(2)如果⊙O的半径为32,ED=2,求AB的长;(3)在(2)的条件
题目详情
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为
(3)在(2)的条件下,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.