如图，P为正方形ABCD内一点，若PA=a，PB=2a，PC=3a（a＞0）．（1）求∠APB的度数；（2）求正方形ABCD的面积．-数学

题目简介

题目详情

如图，P为正方形ABCD内一点，若PA=a，PB=2a，PC=3a（a＞0）．
（1）求∠APB的度数；
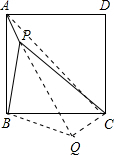
（2）求正方形ABCD的面积． 360优课网

题型：解答题难度：中档来源：不详

答案

（1）将△ABP绕点B顺时针方向旋转90°得△CBQ，如图，
则△ABP≌△CBQ且PB⊥QB，
于是PB=QB=2a，PQ=2

a，
在△PQC中，
∵PC2=9a2，PQ2+QC2=9a2，
∴PC2=PQ2+QC2．
∴∠PQC=90°，
∵△PBQ是等腰直角三角形，
∴∠BPQ=∠BQP=45°，故∠APB=∠CQB=90°+45°=135°；

（2）∵∠APQ=∠APB+∠BPQ=135°+45°=180°，
∴三点A、P、Q在同一直线上，
在Rt△AQC中，AC2=AQ2+QC2=（a+2

a）2+a2=（10+4

）a2，
∴正方形ABCD的面积S=AB2=

AC2

=（5+2

）a2．

如图，P为正方形ABCD内一点，若PA=a，PB=2a，PC=3a（a＞0）．（1）求∠APB的度数；（2）求正方形ABCD的面积．-数学

题目简介

题目详情

答案

更多内容推荐