 如图,∵∠BAC=90°,AB=AC, ∴将△AQC逆时针绕点A旋转90°得△ADB,AC与AB重合,连DP, ∴∠1=∠C,AD=AQ,BD=CQ,∠DAQ=90°, 而∠BAC=90°,AB=AC, ∴∠C=∠ABC=∠1=45°, ∴∠DBP=2∠C=90°, ∴DP2=DB2+BP2, 而QC2+BP2=PQ2, ∴DP=PQ ∴△ADP≌△AQP, ∴∠DAP=∠PAQ, 而∠DAQ=90°, ∴∠PAQ=45°. 故答案为45. |
 如图,∵∠BAC=90°,AB=AC, ∴将△AQC逆时针绕点A旋转90°得△ADB,AC与AB重合,连DP, ∴∠1=∠C,AD=AQ,BD=CQ,∠DAQ=90°, 而∠BAC=90°,AB=AC, ∴∠C=∠ABC=∠1=45°, ∴∠DBP=2∠C=90°, ∴DP2=DB2+BP2, 而QC2+BP2=PQ2, ∴DP=PQ ∴△ADP≌△AQP, ∴∠DAP=∠PAQ, 而∠DAQ=90°, ∴∠PAQ=45°. 故答案为45. |
题目简介
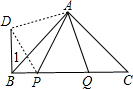
如图,△ABC中,∠BAC=90°,AB=AC,P、Q是BC上两点,且满足BP2+CQ2=PQ2,则∠PAQ的度数是______°.-数学
题目详情