首页 > 如图所示，在半径为a（大小未知）的圆柱空间中（图中圆为其横截面），固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF，其中心O位于圆柱的轴线上．在三角形框架DEF与圆柱-物理

如图所示，在半径为a（大小未知）的圆柱空间中（图中圆为其横截面），固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF，其中心O位于圆柱的轴线上．在三角形框架DEF与圆柱-物理

题目简介

如图所示，在半径为a（大小未知）的圆柱空间中（图中圆为其横截面），固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF，其中心O位于圆柱的轴线上．在三角形框架DEF与圆柱-物理

题目详情

如图所示，在半径为a（大小未知）的圆柱空间中（图中圆为其横截面），固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF，其中心O位于圆柱的轴线上．在三角形框架DEF与圆柱之间的空间中，充满磁感应强度大小为B的均匀磁场，其方向平行于圆柱轴线垂直纸面向里．在EF边上的中点S处有一发射带电粒子的粒子加速器，粒子发射的方向均在截面内且垂直于EF边并指向磁场区域．发射粒子的电量均为q（q＞o），质量均为m，速度大小均为v=
qBL
6m
，若粒子与三角形框架的碰撞均为完全弹性碰撞，且粒子在碰撞过程中所带的电量不变．（不计带电粒子的重力，不计带电粒子之间的相互作用）求：
（1）为使初速度为零的粒子速度增加到v=
qBL
6m
，在粒子加速器中，需要的加速电压为多大；
（2）带电粒子在匀强磁场区域内做匀速圆周运动的半径；．
（3）若满足：从S点发射出的粒子都能再次返回S点，则匀强磁场区域的横截面圆周半径a至少为多大；
（4）若匀强磁场区域的横截面圆周半径a满足第（3）问的条件，则从S点发射出的某带电粒子从S点发射到第一次返回S点的时间是多少？360优课网
题型：问答题难度：中档来源：不详

答案

（1）在粒子加速器中，带电粒子在电场中被加速，根据动能定理可知：qU=class="stub"1
2
mv2
U=
qB2L2
72m
．
（2）带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律可知：qvB=m
v2
r

解得r=class="stub"mv
qB
=class="stub"L
6
．
（3）设想某个带电粒子从S发射后又能回到S，则带电粒子的运动轨迹如图．
当带电粒子的运动轨迹同场区内切时，场区半径有最小值amin．
amin=OG=OF+FG=r+
3
3
L=(class="stub"1
6
+
3
3
)L．
（4）带电粒子在磁场中做匀速圆周运动，由周期公式得：T=class="stub"2πr
v
=class="stub"2πm
qB
．
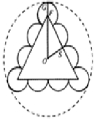360优课网

由轨迹图知，某带电粒子从S发射后第一次返回到S的时间为：t=class="stub"11
2
T=class="stub"11πm
qB
．
答：（1）需要的加速电压为U=
qB2L2
72m
．
（2）带电粒子在匀强磁场区域内做匀速圆周运动的半径class="stub"L
6
．
（3）匀强磁场区域的横截面圆周半径a至少为(class="stub"1
6
+
3
3
)L．
（4）从S点发射出的某带电粒子从S点发射到第一次返回S点的时间是class="stub"11πm
qB
．

更多内容推荐

Copyright © 2018-2020 360优课网