设凸四边形O1O2O3O4的周长为l，以顶点O1，O2，O3，O4为圆心作四个半径为R的圆轮．如果带动四个圆轮转动的皮带长为s，求s的长度（如图）．-数学

题目简介

设凸四边形O₁O₂O₃O₄的周长为l，以顶点O₁，O₂，O₃，O₄为圆心作四个半径为R的圆轮．如果带动四个圆轮转动的皮带长为s，求s的长度（如图）． 360优课网

题型：解答题难度：中档来源：不详

（1）先解一个特例（如图）．设只有两个圆轮⊙O1，⊙O2，2|O1O2|=l'．
显然，带动两轮转动的皮带长度为
s=l'+2πR．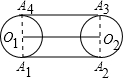

360优课网

（2）再回到原题，我们猜想：
s=l+2πR．
以下证实这个猜想是正确的．
为此，设皮带s与各圆轮接触的四个弧为

A1A8

，

A2A3

，

A4A5

，

A6A7

由于它们是等圆上的弧，因此，只要证出这四条弧恰好组成一个圆即可．
事实上，引O1A'3∥O2A3，由于O1A1∥O2A2，所以∠A1O1A'=∠A2O2A3，∴

A1A3′

A2A3

．同理，
引O1A′6∥O4A6，则

A8A6′

A7A6

．又由于∥O2A3，O2A3∥O1A3′∴O3A4∥O1A3′．同理，O3A5∥O1A′，∴∠A4O3A5=∠A′3O1A′6，∴

A4A5

A′3A′6

∴这四段弧恰好组成一个以O1为圆心，以R为半径的圆．因此，四圆弧之长为2πR．又因为O1O2=A1A2，O2O3=A3A4，O3O4=A5A6，O1O4=A7A8，所以
l=A1A2+A3A4+A5A6+A7A8．
所以，所求皮带长为s=l+2πR．