| 证明:(1)过点M作MH⊥AB于H,MG⊥AD于G,连接AM, ∵M是正方形ABCD的对称中心, ∴M是正方形ABCD对角线的交点, ∴AM平分∠BAD, ∴MH=MG 在正方形ABCD中,∠A=90°, ∵∠MHA=∠MGA=90° ∴∠HMG=90°, 在正方形QMNP,∠EMF=90°, ∴∠EMF=∠HMG. ∴∠FMH=∠EMG, ∵∠MHF=∠MGE. ∴△MHF≌△MGE, ∴MF=ME.(3分) (2)ME=MF.证明:过点M作MH⊥AB于H,MG⊥AD于G,连接AM, ∵M是菱形ABCD的对称中心, ∴M是菱形ABCD对角线的交点,∴AM平分∠BAD, ∴MH=MG, ∵BC∥AD, ∴∠B+∠BAD=180°, ∵∠QMN=∠B, ∴∠QMN+∠BAD=180° 又∵∠MHA=∠MGA=90°,在四边形HMGA中,∠HMG+∠BAD=180°, ∴∠EMF=∠HMG. ∴∠FMH=∠EMG, ∵∠MHF=∠MGE, ∴△MHF≌△MGE, ∴ME=MF.(6分) 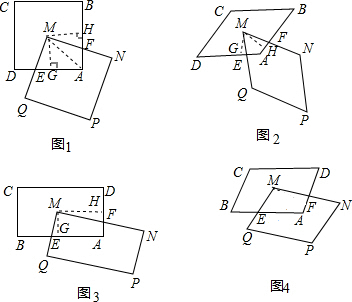 (3)MF=mME. 证明:过点M作MG⊥AB于G,MH⊥AD于H, 在矩形ABCD中,∠A=∠B=90°, ∴∠EMF=∠B=90°, 又∵∠MGA=∠MGE=90°,在四边形GMHA中, ∴∠GMH=90°, ∴∠EMG+∠GMF=∠GMF+∠HMF, ∴∠HMF=∠GME, ∵∠MGE=∠MHF, ∴△MGE∽△MHF, ∴
又∵M是矩形ABCD的对称中心, ∴M是矩形ABCD对角线的中点 ∴MG∥BC, ∴MG=
∵AB=mBC, ∴MF=mME.(9分) (4)平行四边形ABCD和平行四边形QMNP中,∠M=∠B,AB=mBC,M是平行四边形ABCD的对称中心,MN交AD于F,AB交QM于E.则MF=mME.(10分) |
题目简介
如图1,正方形ABCD和正方形QMNP,∠M=∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.(1)求证:ME=MF.(2)如图2,若将原题中的“正方形”改为“菱形”,其他条件不变
题目详情
(1)求证:ME=MF.
(2)如图2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME与线段MF的关系,并加以证明.
(3)如图3,若将原题中的“正方形”改为“矩形”,且AB=mBC,其他条件不变,探索线段ME与线段MF的关系,并说明理
(4)根据前面的探索和图4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.