 ∵DE⊥AB, ∴∠AED=∠BED=90°, ∵DE是∠ADB的平分线, ∴∠3=∠4,又∵DE=DE, ∴△BED≌△AED(ASA), ∴AD=BD,∠2=∠B, ∵∠BAD=∠2=
∴∠1=∠2=∠B, ∴AD=BD, 又∵∠1+∠2+∠B=90°, ∴∠B=∠1=∠2=30°, 在直角三角形ACD中,∠1=30°, ∴CD=
|
 ∵DE⊥AB, ∴∠AED=∠BED=90°, ∵DE是∠ADB的平分线, ∴∠3=∠4,又∵DE=DE, ∴△BED≌△AED(ASA), ∴AD=BD,∠2=∠B, ∵∠BAD=∠2=
∴∠1=∠2=∠B, ∴AD=BD, 又∵∠1+∠2+∠B=90°, ∴∠B=∠1=∠2=30°, 在直角三角形ACD中,∠1=30°, ∴CD=
|
题目简介
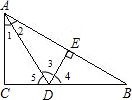
已知:如图,在Rt△ABC中,∠C=90°,∠BAD=12∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=12DB.-数学
题目详情