| 证明:∵∠BAC=90°,CE⊥AE,BD⊥AE, ∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°. ∴∠ABD=∠DAC. ∵在△ABD和△CAE中
∴△ABD≌△CAE(AAS). 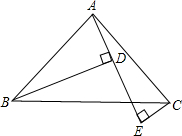 ∴BD=AE,EC=AD. ∵AE=AD+DE, ∴BD=EC+ED. |
| 证明:∵∠BAC=90°,CE⊥AE,BD⊥AE, ∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°. ∴∠ABD=∠DAC. ∵在△ABD和△CAE中
∴△ABD≌△CAE(AAS).  ∴BD=AE,EC=AD. ∵AE=AD+DE, ∴BD=EC+ED. |
题目简介
如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.求证:BD=EC+ED.-数学
题目详情
求证:BD=EC+ED.