已知：点P为线段AB上的动点（与A、B两点不重合）．在同一平面内，把线段AP、BP分别折成△CDP、△EFP，其中∠CDP=∠EFP=90°，且D、P、F三点共线，如图所示．（1）若△CDP、△EFP

题目简介

已知：点P为线段AB上的动点（与A、B两点不重合）．在同一平面内，把线段AP、BP分别折成△CDP、△EFP，其中∠CDP=∠EFP=90°，且D、P、F三点共线，如图所示．
（1）若△CDP、△EFP均为等腰三角形，且DF=2，求AB的长；
（2）若AB=12，tan∠C=

，且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似，求四边形CDFE的面积的最小值． 360优课网

题型：解答题难度：中档来源：海淀区二模

（1）设DP=x，PF=y，
∵△CDP和△EFP都是等腰直角三角形，且∠CDP=∠EFP=90°，
∴CD=DP=x，EF=PF=y，PC=

x，PE=

y．
∴AB=AP+PB=CD+DP+PC+PF+EF+PE
=x+x+

x+y+y+

y
=（2+

）（x+y），
∵DF=2，
∴x+y=2．
∴AB=（2+

）×2=4+2

；

（2）连接CE．
由于tan∠C=class="stub"4

，且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似，因此分两种情况考虑．
①当∠DCP=∠PEF时，
设DP=4m，PF=4n，则CD=3m，EF=3n，
根据勾股定理，可得CP=5m，PE=5n．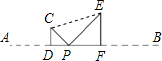
360优课网

∵AB=CD+PC+DP+PE+EF+PF=12（m+n）=12，
∴m+n=1，
∵S四边形CDFE=class="stub"1

（3m+3n）（4m+4n），
=6（m+n）2
=6，
当∠DCP=∠EPF时，
设DP=4m，PF=3n，则CD=3m，EF=4n，
根据勾股定理，可得CP=5m，PE=5n．
∵AB=12（m+n）=12，
∴m+n=1．
∵m＞0，n＞0，
∴S四边形CDFE=class="stub"1

（3m+4n）（4m+3n）
=class="stub"1

(12m2+25mn+12n2)=class="stub"1

[12(m+n)2+mn]
=class="stub"1

（12+mn）
=6+class="stub"1

mn＞6，
综上所述，四边形CDFE的面积的最小值为6．