如图，△ABC中，AB=AC，延长AB到点D，使BD=AB，E是AB的中点，且∠BCE=30°，若BC=m，DC=n，则△BCD的面积为______．-数学

题目简介

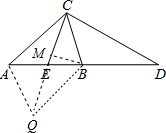
如图，△ABC中，AB=AC，延长AB到点D，使BD=AB，E是AB的中点，且∠BCE=30°，若BC=m，DC=n，则△BCD的面积为______． 360优课网

题型：填空题难度：中档来源：不详

延长CE到Q，使CE=EQ，连接AQ，BQ，过B作BM⊥CE于M，
∵AC=AB，
∴∠ACB=∠ABC，
在△AEC和△BEQ中
∵

AE=BE

∠AEC=∠BEQ

CE=EQ

，
∴△AEC≌△BEQ（SAS），
∴BQ=AC=AB=BD，∠CAB=∠ABQ，
∵∠CBD=∠CAB+∠ACB，∠CBQ=∠ABQ+∠CBA，
又∵∠ACB=∠ABC，
∴∠CBD=∠CBQ，
在△CBQ和△CBD中
∵

CB=CB

∠CBQ=∠CBD

BQ=BD

，
∴△CBQ≌△CBD（SAS），
∴CQ=CD=m，△BCD的面积等于△BCQ面积，
∵在Rt△BMC中，∠BCE=30°，BC=m，
∴BM=class="stub"1

BC=class="stub"1

m，
∴S△BCD=S△BCQ=class="stub"1

CQ×BM=class="stub"1

×n×class="stub"1

m=class="stub"1

mn．
故答案为：class="stub"1

mn．