 ①根据旋转的性质知∠CAD=∠BAF,AD=AF, ∵∠BAC=90°,∠DAE=45°, ∴∠CAD+∠BAE=45°. ∴∠EAF=45°, ∴△AED≌△AEF; 故本选项正确; ②∵AB=AC, ∴∠ABE=∠ACD; ∴当∠BAE=∠CAD时, △ABE∽△ACD, ∴
当∠BAE≠∠CAD时, △ABE与△ACD不相似,即
∴此比例式不一定成立; 故本选项错误; ③根据旋转的性质知△ADC≌△AFB, ∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积; 故本选项正确; ④∵∠FBE=45°+45°=90°, ∴BE2+BF2=EF2, ∵△ADC绕点A顺时针旋转90°后,得到△AFB, ∴△AFB≌△ADC, ∴BF=CD, 又∵EF=DE, ∴BE2+DC2=DE2, 故本选项正确; ⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF, ∴BE+DC=BE+BF>DE=EF,即BE+DC>DE, 故本选项错误; 综上所述,正确的说法是①③④; 故选C. |
题目简介
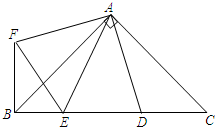
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②AEBE=ADCD;③△A
题目详情
①△AED≌△AEF;②
④BE2+DC2=DE2 ⑤BE+DC=DE
其中正确的是( )