(1) DE与⊙O的位置关系式相切. 理由是:连接OC, ∵AE⊥CD,CF⊥AB,CE=CF, ∴∠EAC=∠CAF, ∵OA=OC, ∴∠CAF=∠OCA, ∴∠OCA=∠EAC, ∴OC∥AE, ∵AE⊥DE, ∴OC⊥DE, ∵OC为⊙O半径, ∴DE是⊙O的切线, 即DE与⊙O的位置关系式相切. (2)  ∵OC⊥DE, ∴∠OCD=90°, ∵AB=6,BD=3, ∴OB=3=BD, 即B为OD中点, ∴CB=OB=BD=3, ∵AB是直径, ∴∠ACB=90°, 在△ACB中,AB=6,BC=3,由勾股定理得:AC=3
在△ACB中,由三角形的面积公式得:
∴
CF=
∵CE=CF, ∴CE=
在Rt△AEC中,AC=3
即AE=
|
题目简介
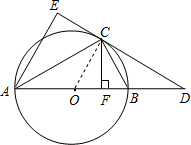
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.(1)判断DE与⊙O的位置关系,并说明理由;(2)若AB=6,B
题目详情
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若AB=6,BD=3,求BC和AE的长.