| (1)证明:连接OP. ∵四边形BCEF是正方形, 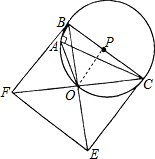 ∴BE⊥CF,OB=OC. ∵P是BC的中点, ∴OP=
∵BC是圆的直径, ∴点O在圆上. ∴∠BAO=90°+45°=135°. (2)过O作OK⊥BA延长线于K. ∵AO=4
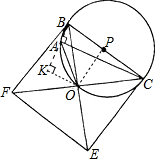 ∴∠BAO=135°, ∴∠OAK=45°, ∴AK=OK=4. 根据勾股定理,得 BO=2
∴AC=10. |
| (1)证明:连接OP. ∵四边形BCEF是正方形,  ∴BE⊥CF,OB=OC. ∵P是BC的中点, ∴OP=
∵BC是圆的直径, ∴点O在圆上. ∴∠BAO=90°+45°=135°. (2)过O作OK⊥BA延长线于K. ∵AO=4
 ∴∠BAO=135°, ∴∠OAK=45°, ∴AK=OK=4. 根据勾股定理,得 BO=2
∴AC=10. |
题目简介
如图,以BC为直径作Rt△ABC的外接圆,圆心为点P,在△ABC的同侧又作正方形BCEF,BE、CF交于点为O,连接AO.(1)求证:点O在⊙P上且∠BAO=135°;(2)如果AB=2,AO=42,
题目详情
(1)求证:点O在⊙P上且∠BAO=135°;
(2)如果AB=2,AO=4