 证明:(1)∵∠C=90°,CD⊥AB,∠A=60°, ∴∠ACD=∠B=30°, ∵∠C=90°,CD⊥AB, ∴AB=2AC,AC=2AD, ∴AB=4AD, ∴BD=3AD. (2)取AB的中点O,连接CO, ∵BD=3AD, ∴设AD=x,则BD=3x,AB=4x, ∵∠C=90°,O是AB的中点, ∴OC=OA=2x, ∴OD=x=
∵CD⊥AB, ∴∠OCD=30°, ∴∠COD=60°, ∵OA=OC, ∴△ACO是等边三角形, ∴∠A=60°. |
 证明:(1)∵∠C=90°,CD⊥AB,∠A=60°, ∴∠ACD=∠B=30°, ∵∠C=90°,CD⊥AB, ∴AB=2AC,AC=2AD, ∴AB=4AD, ∴BD=3AD. (2)取AB的中点O,连接CO, ∵BD=3AD, ∴设AD=x,则BD=3x,AB=4x, ∵∠C=90°,O是AB的中点, ∴OC=OA=2x, ∴OD=x=
∵CD⊥AB, ∴∠OCD=30°, ∴∠COD=60°, ∵OA=OC, ∴△ACO是等边三角形, ∴∠A=60°. |
题目简介
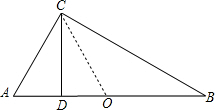
在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D.(1)如果∠A=60°,求证:BD=3AD;(2)如果BD=3AD,求证:∠A=60°.-数学
题目详情
(1)如果∠A=60°,求证:BD=3AD;
(2)如果BD=3AD,求证:∠A=60°.