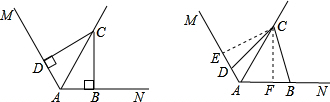已知∠MAN，AC平分∠MAN．（1）在图1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：AB+AD=AC；（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中

题目简介

已知∠MAN，AC平分∠MAN．
（1）在图1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：AB+AD=AC；
（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

360优课网

题型：解答题难度：中档来源：不详

（1）证明：∵∠MAN=120°，AC平分∠MAN，
∴∠CAD=∠CAB=60°．
又∠ABC=∠ADC=90°，
∴AD=class="stub"1

AC，AB=class="stub"1

AC，
∴AB+AD=AC．

（2）结论仍成立．理由如下：
作CE⊥AM、CF⊥AN于E、F．则∠CED=∠CFB=90°，
∵AC平分∠MAN，
∴CE=CF．
∵∠ABC+∠ADC=180°，∠ADC+∠CDE=180°
∴∠CDE=∠ABC，
在△CDE和△CBF中，

∠CDE=∠CBF

∠CED=∠CFB

CE=CF

，
∴△CDE≌△CBF（AAS），
∴DE=BF．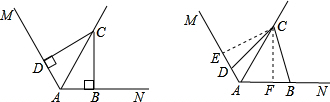

360优课网

∵∠MAN=120°，AC平分∠MAN，
∴∠MAC=∠NAC=60°，∴∠ECA=∠FCA=30°，
在Rt△ACE与Rt△ACF中，则有AE=class="stub"1

AC，AF=class="stub"1

AC，
则AD+AB=AD+AF+BF=AD+AF+DE=AE+AF=class="stub"1

AC+class="stub"1

AC=AC．
∴AD+AB=AC．