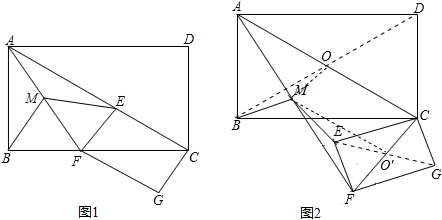
 (1)证明:如图1. ∵四边形ABCD是矩形,四边形EFGC是矩形, ∴∠ABF=90°,∠FEC=90°=∠AEF, ∵M为AF中点, ∴BM=
∴BM=EM; (2)若将(1)中的矩形EFGC绕着点C旋转一定的角度,其它条件不变,则(1)中的结论还成立,理由如下:如图2. 证明:设大小矩形的中心分别为O、O′,连接BD,OM,MO′,EG. ∵M,O′分别为AF,CF的中点, ∴MO′=
∵∠ACB=∠ECF, ∴∠OAB=∠EFO′, 又∵OB=
∴∠OAB=∠OBA; 同理可证∠EFO′=∠FEO′. ∴∠AOB=∠EO′F,① 又∵OM∥CF,MO′∥AC, ∴∠AOM=∠OCF=∠MO′F,② 由①,②得:∠BOM=∠MO′E, 在△BMO与△MEO′中,
∴△BMO≌△MEO′(SAS), ∴BM=ME. |
题目简介
已知矩形EFGC(如图1)的一边EC和对角线CF分别与矩形ABCD的对角线AC及边BC重合.连接AF,取AF的中点为M,连接BM、EM.(1)求证:MB=ME;(2)如图2,若将(1)中的矩形EFGC
题目详情
(1)求证:MB=ME;
(2)如图2,若将(1)中的矩形EFGC绕着点C旋转一定的角度,其它条件不变,你认为(1)中的结论是否还成立?若成立请证明;若不成立,请说明理由.