 (1)△ABD是等腰直角三角形.理由如下: ∵AB是圆O的直径, ∴∠ADB=90°, ∵CD平分∠ACB, ∴
∴AD=BD, ∴△ABD是等腰直角三角形; (2)DI的长度不变,且DI=5
在Rt△ABD中, ∵AD=BD,AB=10, ∴BD=5
连接OI, ∵I是△ABC的内心, ∴∠4=∠5, ∵由(1)可知
∴∠1=∠2, ∵∠3是△BCI的外角, ∴∠3=∠1+∠4=∠2+∠5, ∴DI=BD是定值,即DI=BD=5
|
 (1)△ABD是等腰直角三角形.理由如下: ∵AB是圆O的直径, ∴∠ADB=90°, ∵CD平分∠ACB, ∴
∴AD=BD, ∴△ABD是等腰直角三角形; (2)DI的长度不变,且DI=5
在Rt△ABD中, ∵AD=BD,AB=10, ∴BD=5
连接OI, ∵I是△ABC的内心, ∴∠4=∠5, ∵由(1)可知
∴∠1=∠2, ∵∠3是△BCI的外角, ∴∠3=∠1+∠4=∠2+∠5, ∴DI=BD是定值,即DI=BD=5
|
题目简介
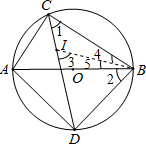
如图,AB是圆O的直径,AB=10,点C是圆O上一动点(与A,B不重合),∠ACB的平分线交圆O于D.(1)判断△ABD的形状,并证明你的结论;(2)若I是△ABC的内心,当点C运动时,CI、DI中是
题目详情
(1)判断△ABD的形状,并证明你的结论;
(2)若I是△ABC的内心,当点C运动时,CI、DI中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.