| (1)连接AC, ∵等腰梯形ABCD, ∴BD=AC, 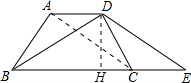 ∵AD=CE, ∴四边形ACED是平行四边形, ∴AC=DE, ∴BD=DC, (2)过D作DH⊥BC于H, ∵BD平分∠ABC, ∴∠ABD=∠ADB, ∵AD∥BC, ∴∠ADC=∠CBD, ∴∠ABD=∠ADB, ∴AB=AD=DC=2, ∵∠ABC=∠DCB,BD⊥DC, ∴∠DCB+DAC=90°, ∴∠DCB=60°, ∴BC=2DC=4, ∴HC=
∴求梯形面积是
|
| (1)连接AC, ∵等腰梯形ABCD, ∴BD=AC,  ∵AD=CE, ∴四边形ACED是平行四边形, ∴AC=DE, ∴BD=DC, (2)过D作DH⊥BC于H, ∵BD平分∠ABC, ∴∠ABD=∠ADB, ∵AD∥BC, ∴∠ADC=∠CBD, ∴∠ABD=∠ADB, ∴AB=AD=DC=2, ∵∠ABC=∠DCB,BD⊥DC, ∴∠DCB+DAC=90°, ∴∠DCB=60°, ∴BC=2DC=4, ∴HC=
∴求梯形面积是
|
题目简介
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.(1)求证:BD=DE;(2)当DC=2时,求梯形面积.-数学
题目详情
(1)求证:BD=DE;
(2)当DC=2时,求梯形面积.