 证明:(1)在△ADE中, ∵AD=AE,F是DE的中点, ∴AF是等腰△ADE底边DE上的中线, ∴AF⊥DE.(2分) (2)连接GC. ∵AF⊥DE,H是AC的中点, ∴FH是Rt△AFC斜边AC上的中线, ∴FH=
同理:GH=
∴FH=GH.(5分) |
 证明:(1)在△ADE中, ∵AD=AE,F是DE的中点, ∴AF是等腰△ADE底边DE上的中线, ∴AF⊥DE.(2分) (2)连接GC. ∵AF⊥DE,H是AC的中点, ∴FH是Rt△AFC斜边AC上的中线, ∴FH=
同理:GH=
∴FH=GH.(5分) |
题目简介
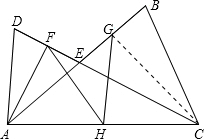
如图,AB、CD交于点E,AD=AE,CB=CE,F、G、H分别是DE、BE、AC的中点.(1)求证:AF⊥DE;(2)求证:FH=GH.-数学
题目详情
(1)求证:AF⊥DE;
(2)求证:FH=GH.