如图，在△ABC中，∠BAC=90°，且AB=AC，∠ABC=∠ACB=45°，点D是AC的中点，AE⊥BD于点F，交BC于点E，连接DE．求证：（1）∠BAF=∠ADB；（2）∠ADB=∠EDC．-

题目简介

如图，在△ABC中，∠BAC=90°，且AB=AC，∠ABC=∠ACB=45°，点D是AC的中点，AE⊥BD于点F，交BC于点E，连接DE．
求证：（1）∠BAF=∠ADB；
（2）∠ADB=∠EDC． 360优课网

题型：解答题难度：中档来源：不详

（1）证明：∵∠BAC=90°，
∴∠BAF+∠DAF=90°，
∵AE⊥BD，
∴∠AFD=90°，
∴∠DAF+∠ADB=90°，
∴∠BAF=∠ADB．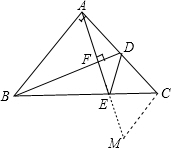

360优课网

（2）证明：过C作CM⊥AC，交AE的延长线于M，
则∠ACM=90°=∠BAC，
∴CM∥AB，
∴∠MCE=∠ABC=∠ACB，
∵∠BAF=∠ADB，∠ADB+∠FAD=90°，∠ABD+∠BAF=90°，
∴∠ABD=∠CAM，
在△ABD和△CAM中
∵

∠DAB=∠ACM

AB=AC

∠ABD=∠CAM

，
∴△ABD≌△CAM（ASA），
∴∠ADB=∠M，AD=CM，
∵D为AC中点，
∴AD=DC=CM，
在△CDE和△CME中，
∵

CD=CM

∠DCE=∠MCE

CE=CE

，
∴△CDE≌△CME（SAS），
∴∠M=∠EDC，
∵∠M=∠ADB，
∴∠ADB=∠EDC．