首页 > 如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．（1）判断DE与⊙O的位置关系并说明理由；（2）若tanC=52，DE=2，求AD的长．-数学

如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．（1）判断DE与⊙O的位置关系并说明理由；（2）若tanC=52，DE=2，求AD的长．-数学

题目简介

如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．（1）判断DE与⊙O的位置关系并说明理由；（2）若tanC=52，DE=2，求AD的长．-数学

题目详情

如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．
（1）判断DE与⊙O的位置关系并说明理由；
（2）若tanC=
5
2
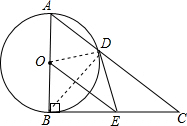，DE=2，求AD的长．360优课网
题型：解答题难度：中档来源：兰州

答案

（1）DE与⊙O相切，

360优课网


理由如下：连接OD，BD，
∵AB是直径，
∴∠ADB=∠BDC=90°，
∵E是BC的中点，
∴DE=BE=CE（直角三角形斜边上的中线等于斜边的一半），
∴∠EDB=∠EBD，
∵OD=OB，
∴∠OBD=∠ODB，
∴∠OBD+∠DBE=∠ODB+∠EDB，
即∠EDO=∠EBO=90°，
∴OD⊥DE，
∵OD是半径，
∴DE与⊙O相切．

（2）∵tanC=
5
2
=class="stub"BD
DC
，可设BD=
5
x，CD=2x，

360优课网


∵在Rt△BCD中，BC=2DE=4，BD2+CD2=BC2
∴（
5
x）2+（2x）2=16，
解得：x=±class="stub"4
3
（负值舍去）
∴BD=
5
x=class="stub"4
3
5
，
∵∠ABD+∠DBC=90°，∠C+∠DBC=90°，
∴∠ABD=∠C，
∴tan∠ABD=tanC，
∵tan∠ABD=class="stub"AD
BD
=
5
2
，
AD=
5
2
BD=
5
2
×
4
5
3
=class="stub"10
3
．
答：AD的长是class="stub"10
3
．

更多内容推荐

Copyright © 2018-2020 360优课网