| (1)根据题意得:A′C=BD,∠BDC=∠A′CD, ∴A′C∥BD, ∴四边形A′BCD一定是平行四边形; 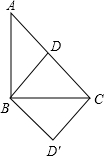 (2)将AB边与BC边重合, ∵BD是等腰直角三角形ABC斜边上的高, ∴AD=CD=BD=
∴BD=CD=CD′=BD′, ∴四边形BDCD′是菱形, ∵∠BDC=90°, ∴四边形BDCD′是正方形; 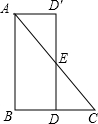 (3)分别取AC于BC的中点,沿DE剪下△DEC, ∴DE∥AB, ∵△ABC是直角三角形, ∴∠B=90°, ∴∠AD′E=∠EDC=∠EDB=∠B=90°, ∴四边形AD′DB是矩形. |
题目简介
(1)如图,把一个等腰直角△ABC沿斜边上的高BD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分拼成一个四边形A′BCD(见示意图A).①猜一猜,四边形A′BCD一定是______形.②试-数
题目详情
①猜一猜,四边形A′BCD一定是______形.
②试一试,按上述裁剪方法,请你拼一个与图A形状不同的四边形,并在图B中画出示意图.
(2)在等腰直角三角形△ABC中,请你找出与(1)不同的裁剪线,把分割成的两部分拼成一个特殊的四边形,请你在图C中画出你拼得的特殊的四边形的示意图.