 (1)∵AD∥BC, ∴∠FGC=∠D=90°, ∵∠C=30°, ∴∠AFD=∠CFG=60°, ∴∠DAF=30°, ∵∠DAE=45°, ∴∠CAE=15°, ∴当α为 15度时,AD∥BC; (2)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的度数是:15°,45°,105°,135°,150°; 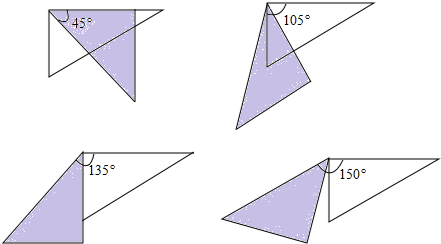 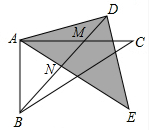 (3)当0°<α<45°,∠BDE+∠CAE+∠DBC=105°,保持不变; 理由如下: 设BD分别交AC、AE于点M、N, 在△AMN中,∠AMN+∠CAE+∠ANM=180, ∵∠ANM=∠E+∠BDE,∠AMN=∠C+∠DBC, ∴∠E+∠BDE+∠CAE+∠C+∠DBC=180°, ∵∠C=30°,∠E=45°, ∴∠BDE+∠CAE+∠DBC=105°; |
题目简介
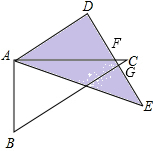
如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).(1)当α为______度时,AD∥BC,并
题目详情
(1)当α为______度时,AD∥BC,并在图3中画出相应的图形;
(2)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(3)当0°<α<45°,连接BD,利用图4探究∠BDE+∠CAE+∠DBC的度数是否发生变化,并给出你的证明.