| (1)AD⊥BE,AD=BE, ∵等腰直角△ABC和等腰直角△CDE, ∴DC=EC,∠DCA=∠ECB,AC=BC, ∴△BEC≌△ADC, ∴AD=BE,∠DAC=∠EBC,又∠BEC=∠AEF,∠BEC+∠EBC=90°, ∴∠AEF+∠DAC=90°, ∴∠AFB=90°, ∴AD⊥BE. (2)仍存在.如图, 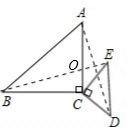 ∵等腰直角△ABC和等腰直角△CDE, ∴DC=EC,AC=BC,∠DCE=∠ACB, ∴∠DCA=∠ECB, ∴△BEC≌△ADC ∴AD=BE,∠DAC=∠EBC,又∠BOC=∠AOE,∠BOC+∠EBC=90°, ∴∠AOE+∠DAC=90°, ∴AD⊥BE. |
题目简介
(1)等腰直角△ABC和等腰直角△CDE的位置如图所示,连接BE,并延长交AD于F,试问AD与BE之间有什么关系?证明你的结论;(2)若保持其他条件不变,等腰直角△CDE绕C点旋转,位置如下-数学
题目详情
(2)若保持其他条件不变,等腰直角△CDE绕C点旋转,位置如下图所示,试问AD与BE之间的关系还存在吗?若存在,给予证明;若不存在,则说明理由.