 证明:(1)∵点E是DC中点∴DE=CE(1分) 又∵AD∥BC,F在AD延长线上,∴∠DFE=∠EBC,∠FDE=∠ECB(3分) 在△BCE与△FDE中
∴△BCE≌△FDE(AAS)(6分) (2)四边形BCFD是平行四边形.理由如下:(7分) ∵△BCE≌△FDE, ∴DE=CE,FE=BE.(9分) ∴四边形BCFD是平行四边形.(10分). |
 证明:(1)∵点E是DC中点∴DE=CE(1分) 又∵AD∥BC,F在AD延长线上,∴∠DFE=∠EBC,∠FDE=∠ECB(3分) 在△BCE与△FDE中
∴△BCE≌△FDE(AAS)(6分) (2)四边形BCFD是平行四边形.理由如下:(7分) ∵△BCE≌△FDE, ∴DE=CE,FE=BE.(9分) ∴四边形BCFD是平行四边形.(10分). |
题目简介
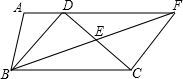
已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于点F.(1)求证:△BCE≌△FDE.(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.-数学
题目详情
点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.