如图1，△ABC中，∠BAC=90°，BA=AC，（1）D为AC的中点，连BD，过A点作AE⊥BD于E点，交BC于F点，连DF，求证：∠ADB=∠CDF．（2）若D，M为AC上的三等分点，如图2，连B

题目简介

题目详情

如图1，△ABC中，∠BAC=90°，BA=AC，
（1）D为AC的中点，连BD，过A点作AE⊥BD于E点，交BC于F点，连DF，求证：∠ADB=∠CDF．
（2）若D，M为AC上的三等分点，如图2，连BD，过A作AE⊥BD于点E，交BC于点F，连MF，判断∠ADB与∠CMF的大小关系并证明．

360优课网

题型：解答题难度：中档来源：不详

答案

（1）证明：作AG平分∠BAC，交BD于点G
∵∠BAC=90°，AE⊥BD，
∴∠DAE+∠ADB=∠ABE+∠ADB=90°，
∴∠ABG=∠CAF，
∵△ABC是等腰直角三角形，
∴AB=AC，∠C=∠BAG=45°，
∴

∠ABG=∠CAF

AB=AC

∠C=∠BAG=45°

∴△BAG≌△CAF，（ASA）
∴AG=CF，
又∵AD=CD，∠GAD=∠C=45°，
∴△AGD≌△DFC，（SAS）
∴∠ADB=∠CDF；

（2）∠ADB=∠CMF．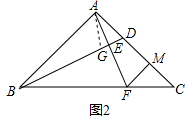
360优课网

证明：作AG平分∠BAC，交BD于点G
∵∠BAC=90°，AE⊥BD，
∴∠DAE+∠ADB=∠ABE+∠ADB=90°，
∴∠ABG=∠CAF，
∵△ABC是等腰直角三角形，
∴AB=AC，∠C=∠BAG=45°，
∴

∠ABG=∠CAF

AB=AC

∠C=∠BAG=45°

∴△BAG≌△CAF，（ASA）
∴AG=CF，
又∵AD=CM，∠GAD=∠C=45°，
∴△AGD≌△CFM，（SAS）
∴∠ADG=∠CMF；
即：∠ADB=∠CMF．

上一篇 : 下列关于人体发育的叙述错误的
下一篇 : 如图：在△ABC中，∠C=90度，AC=BC，BD

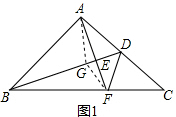
如图1，△ABC中，∠BAC=90°，BA=AC，（1）D为AC的中点，连BD，过A点作AE⊥BD于E点，交BC于F点，连DF，求证：∠ADB=∠CDF．（2）若D，M为AC上的三等分点，如图2，连B

题目简介

题目详情

答案

更多内容推荐