| (1)∵AB=AC,AO是∠BAC的角平分线, ∴AO⊥BC, ∴∠AOC=90°,BO=OC, ∵∠BAC=90°, ∴BO=OA=OC; (2)S△AOA1=S△BOC1 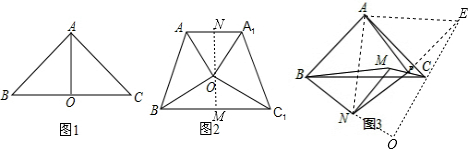 . 证明:过点O作MN⊥BC1于M,交AA1于N, ∵OB=OC1, ∴BM=C1M,∠BOM=∠C1OM, ∵∠AOB=∠A1OC1=90°, ∴∠AON+∠BOM=∠A1ON+∠C1OM=90°, ∴∠AON=∠A1ON, ∵AO=A1O, ∴ON⊥AA1, ∴∠A1NO=90°=∠OMC1, ∵在△OMC1和△A1ON中
∴△A1ON≌△OC1M(AAS), ∴△A1ON和△OC1M的面积相等, 同理可证△AON和△OBM的面积相等, ∴S△AOA1=S△BOC1; (3)证明:延长NP至E,使PE=NP,连接CE,AN,AE, ∵点P为MC的中点, ∴MP=CP, ∵在△PCE和△PMN中
∴△PCE≌△PMN(SAS), ∴CE=NM=BN,∠MNP=∠PEC, ∴CE∥MN, 设EC的延长线交BN的延长线于O, ∴∠BNM=∠BOC=90°, 又∵∠BAC=90°, ∴A、B、O、C四点共圆, ∴在四边形ABOC中,∠ACE=∠ABN, ∵在△ABN和△ACE中
∴△ABN≌△ACE(SAS), ∴AN=AE,∠ABN=∠EAC, ∵∠BAC=90°=∠BAN+∠NAC=∠EAC+∠NAC=∠EAN, 即∠EAN=90°, ∵点P为NE的中点, ∴PA=PN(直角三角形斜边上中线等于斜边的一半). |
题目简介
如图1,已知AO是等腰Rt△ABC的角平分线,∠BAC=90°,AB=AC.(1)在图1中,∠AOC的度数为______;与线段BO相等的线段为______;(2)将图1中的△AOC绕点O顺时针旋转得
题目详情
(1)在图1中,∠AOC的度数为______;与线段BO相等的线段为______;
(2)将图1中的△AOC绕点O顺时针旋转得到△A1OC1,如图2,连接AA1,BC1,试判断S△AOA1与S△BOC1的大小关系?并给出你的证明;
(3)将图1中的△ABO绕点B顺时针旋转得到△MBN,如图3,点P为MC的中点,连接PA、PN,求证:PA=PN.