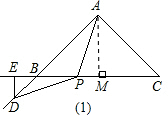
 (1)如图,过点A作AM⊥BC,垂足为M, ∵∠BAC=90°,AB=AC,∴∠ABC=∠C=45°, ∵PA=PD,∴∠BAP=∠PDB, ∵DE⊥BC,∴∠BDE=∠EBD=45°, ∴∠APM=∠PDE, ∴△PDE≌△APM,∴PM=DE, ∵ED=BE,∴PM=BE, ∴PE=BM=
(2)如图,点P在CB的延长线上, 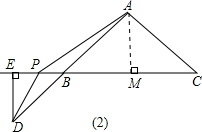 当点P分别放在点P在BC的延长线上时不成立; (3)当点P分别放在点P在CB的延长线上, 如(2)中图,如图,过点A作AM⊥BC,垂足为M, ∵∠BAC=90°,AB=AC,∴∠ABC=∠C=45°, ∵PA=PD,∴∠BAP=∠PDB, ∵DE⊥BC,∴∠BDE=∠EBD=45°, ∴∠APM=∠PDE, ∴△PDE≌△APM,∴PM=DE, ∵ED=BE,∴PM=BE, ∴PE=BM=
此时成立, 当点P分别放在点P在BC的延长线上时, ∵PA=PD,∴∠BAP=∠PDB, ∵∠BAP=∠PDB>90°, ∴由三角形的内角和定理得, 当点P分别放在点P在BC的延长线上时不成立. |
题目简介
如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为BC所在直线上一点,D为AB所在直线上一点,操作:当PA=PD时,过点D作BC所在直线的垂线,垂足为E.(1)猜测线段PE与线段BC的数量关系
题目详情
(1)猜测线段PE与线段BC的数量关系;
(2)请你利用图②,图③,选择不同位置的点P、D按上述方法操作;
(3)经历(2)之后,如果认为你猜测的结论是正确的,请加以证明;如果认为你猜测的结论是错误的,请说明理由.