| (1)证明:由题意得:AC=CD=DA, ∵∠ACB=90°, ∴△ACD是等边三角形, 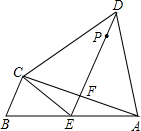 ∵DE⊥AC, ∴DE垂直平分AC, ∴AE=CE, ∵∠ACB=90°, ∴∠ACE+∠BCE=∠CAE+∠B=90°, ∴∠BCE=∠B, ∴BE=CE; ∴AE=CE=BE; (2)∵DE垂直平分AC, ∴PC=PA, ∴PB+PC=PB+PA; ∴PB+PC最小,也就是PB+PA最小,也就是P、B、A在同一直线上是最小, 即当P在E处时最小, 当点P在E处时,PB+PC=AB=35米. |
| (1)证明:由题意得:AC=CD=DA, ∵∠ACB=90°, ∴△ACD是等边三角形,  ∵DE⊥AC, ∴DE垂直平分AC, ∴AE=CE, ∵∠ACB=90°, ∴∠ACE+∠BCE=∠CAE+∠B=90°, ∴∠BCE=∠B, ∴BE=CE; ∴AE=CE=BE; (2)∵DE垂直平分AC, ∴PC=PA, ∴PB+PC=PB+PA; ∴PB+PC最小,也就是PB+PA最小,也就是P、B、A在同一直线上是最小, 即当P在E处时最小, 当点P在E处时,PB+PC=AB=35米. |
题目简介
某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路-数学
题目详情
(1)说明:AE=CE=BE;
(2)若AB=35m,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时,PB+PC的值.