| (1))△ADE≌△BEC. 证明:∵AD∥BC,∠A=90°, 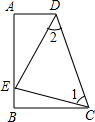 ∴∠B=∠A=90°, ∵∠1=∠2, ∴DE=CE, ∵在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL); (2)△CED是等腰直角三角形. ∵Rt△ADE≌Rt△BEC, ∴∠ADE=∠BEC, ∵∠A=90°, ∴∠ADE+∠AED=90°, ∴∠BEC+∠AED=90°, ∴∠CDE=90°, 又∵DE=CE, ∴△CED是等腰直角三角形. |
| (1))△ADE≌△BEC. 证明:∵AD∥BC,∠A=90°,  ∴∠B=∠A=90°, ∵∠1=∠2, ∴DE=CE, ∵在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL); (2)△CED是等腰直角三角形. ∵Rt△ADE≌Rt△BEC, ∴∠ADE=∠BEC, ∵∠A=90°, ∴∠ADE+∠AED=90°, ∴∠BEC+∠AED=90°, ∴∠CDE=90°, 又∵DE=CE, ∴△CED是等腰直角三角形. |
题目简介
如图,已知AD∥BC,∠A=90°,E为AB上一点,且AE=BC,∠1=∠2.请说明:(1)△ADE与△BEC全等吗?请说明理由;(2)判断△CDE的形状,并说明理由.-数学
题目详情
(1)△ADE与△BEC全等吗?请说明理由;
(2)判断△CDE的形状,并说明理由.