| 本题有两种情形: (1)当点A是绳子的对折点时,将绳子展开如图. ∵AP:BP=2:3,剪断后的各段绳子中最长的一段为60cm, ∴2AP=60cm, ∴AP=30cm, ∴PB=45cm, ∴绳子的原长=2AB=2(AP+PB)=2×(30+45)=150(cm);  (2)当点B是绳子的对折点时,将绳子展开如图. ∵AP:BP=2:3,剪断后的各段绳子中最长的一段为60cm, ∴2BP=60cm, ∴BP=30cm, ∴AP=20cm. ∴绳子的原长=2AB=2(AP+BP)=2×(20+30)=100(cm). 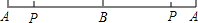 综上,绳子的原长为150cm或100cm. |
题目简介
如图所示,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60cm,求绳子的原长.-数学
题目详情