首页 > 如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强-物理

如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强-物理

题目简介

如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强-物理

题目详情

如图所示，在空间中有一坐标系oxy，其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ．直线OP是它们的边界．区域Ⅰ中的磁感应强度为2B，方向垂直纸面向内，区域Ⅱ中的磁感应强度为B，方向垂直纸面向外，边界上的P点坐标为（3L，3L）．一质量为m，电荷量为+q的粒子从P点平行于y轴正方向以速度v0=
2BqL
m
射入区域Ⅰ，经区域Ⅰ偏转后进入区域Ⅱ（忽略粒子重力），求：
（1）粒子在Ⅰ和Ⅱ两磁场中做圆周运动的半径之比；
（2）粒子在磁场中运动的总时间及离开磁场的位置坐标．360优课网
题型：问答题难度：中档来源：不详

答案

（1）带电粒子射入磁场中，由洛伦兹力提供向心力而做匀速圆周运动，根据牛顿第二定律得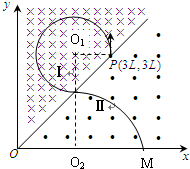
360优课网

    qvB=m
v2
R
  ①
解得 R=class="stub"mv
qB
    ②
所以，粒子在Ⅰ和Ⅱ两磁场中做圆周运动的半径分别为：R1=
mv0
2qB
，R2=
mv0
qB
    ③
解得
R1
R2
=class="stub"1
2
    ④
（2）粒子在磁场中圆周运动的周期为T=class="stub"2πm
qB
   ⑤
可得 T1=class="stub"πm
qB
，T2=class="stub"2πm
qB
            ⑥
粒子在区域Ⅰ中转过的圆心角为θ1=class="stub"3
2
π    ⑦
粒子在区域Ⅰ中运动的时间为t1=
θ1
2π
T1   ⑧
解得t1=class="stub"3πm
4qB
      ⑨
粒子在区域Ⅱ中转过的圆心角为θ2=class="stub"π
2
       ⑩
粒子在区域Ⅱ中运动的时间为t2=
θ2
2π
T2     （11）
解得t2=class="stub"πm
2qB
            （12）
所以t=t1+t2=class="stub"5πm
4qB
      （13）
将速度v0=class="stub"2BqL
m
代入得
  R1=L，R2=2L       （14）
由几何关系得
.
OO2
=3L-R1，
.
O2M
=R2               （15）
粒子离开磁场的横坐标为x=
.
OO2
+
.
O2M
=4L      （16）
粒子离开磁场的位置坐标（4L，0）（17）
答：（1）粒子在Ⅰ和Ⅱ两磁场中做圆周运动的半径之比是1：2；
（2）粒子在磁场中运动的总时间是class="stub"5πm
4qB
，离开磁场的位置坐标是（4L，0）．

更多内容推荐

Copyright © 2018-2020 360优课网