| (1)由题意可知,微粒所受的重力 G=mg=8×10-3N 电场力大小F=Eq=8×10-3N 因此重力与电场力平衡 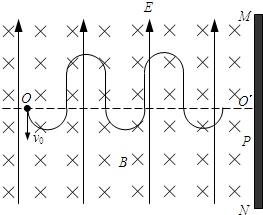 微粒先在洛伦兹力作用下做匀速圆周运动,则qvB=m
解得 R=
由 T=
解得T=10πs 则微粒在5πs内转过半个圆周,再次经直线OO′时与O点的距离 l=2R=1.2m (2)微粒运动半周后向上匀速运动,运动的时间为t=5πs,轨迹如图所示,位移大小 s=vt=0.6πm=1.88m 因此,微粒离开直线OO′的最大高度 h=s+R=2.48m (3)若微粒能垂直射到挡板上的某点P,P点在直线OO′下方时,由图象可知,挡板MN与O点间的距离应满足 L=(2.4n+0.6)m(n=0,1,2…) 若微粒能垂直射到挡板上的某点P,P点在直线OO′上方时,由图象可知,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…) 答:(1)微粒再次经过直线OO′时与O点的距离为1.2m. (2)微粒在运动过程中离开直线OO′的最大高度为2.48m. (3)若微粒能垂直射到挡板上的某点P,P点在直线OO′下方时,挡板MN与O点间的距离应满足L=(2.4n+0.6)m(n=0,1,2…) 若微粒能垂直射到挡板上的某点P,P点在直线OO′上方时,挡板MN与O点间的距离应满足 L=(2.4n+1.8)m (n=0,1,2…) |
题目简介
如图甲所示,竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,电场和磁场的范围足够大,电场强度E=40N/C,磁感应强度B随时间t变化的关系图象如图-物理
题目详情
(1)微粒再次经过直线OO′时与O点的距离;
(2)微粒在运动过程中离开直线OO′的最大高度;
(3)水平移动挡板,使微粒能垂直到挡板上,挡板与O点间的距离应满足的条件.