 证明:2BF=CE,且BF⊥CE. 过点E作EG⊥CB的延长线于点G.可得BDEG是矩形,即BD=EG,BG=DE, 设BC=AD=m,AB=DE=n. ∵BF是∠ABC的平分线, ∴∠DBF=45°, 又∵DF⊥BF, ∴∠FDB=45°, ∴△BFD是等腰直角三角形, ∴BF2+DF2=BD2,BF2+BF2=(AB+AD)2=(m+n)2, ∴BF=
又∵△CGE也是直角三角形, ∴CE2=CG2+GE2 =(CB+BG)2+BD2 =(CB+DE)2+(AB+AD)2 =(m+n)2+(m+n)2 =2(m+n)2 ∴CE=
由此可得,2BF=CE; ∵∠GCE=∠CBF=45°, ∴CE⊥BF. |
题目简介
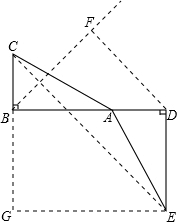
两个全等的Rt△ABC和Rt△EDA如图放置,点B、A、D在同一条直线上.操作:在图中,作∠ABC的平分线BF,过点D作DF⊥BF,垂足为F,连接CE.证明BF⊥CE.探究:线段BF、CE的关系,并证
题目详情
操作:在图中,作∠ABC的平分线BF,过点D作DF⊥BF,垂足为F,连接CE.证明BF⊥CE.
探究:线段BF、CE的关系,并证明你的结论.
说明:如果你无法证明探究所得的结论,可以将“两个全等的Rt△ABC和Rt△EDA”改为“两个全等的等腰直角△ABC和等腰直角△EDA(点C、A、E在同一条直线上)”,其他条件不变,完成你的证明,此证明过程最多得2分.