 (1)图中是通过绕点A旋转90°,使△ABE变到△ADF的位置. 证明:(2)BE=DF,BE⊥DF; 延长BE交DF于G; 由△ABE≌△ADF,得BE=DF,∠ABE=∠ADF; 又∠AEB=∠DEG; ∴∠DGB=∠DAB=90°; ∴BE⊥DF. |
 (1)图中是通过绕点A旋转90°,使△ABE变到△ADF的位置. 证明:(2)BE=DF,BE⊥DF; 延长BE交DF于G; 由△ABE≌△ADF,得BE=DF,∠ABE=∠ADF; 又∠AEB=∠DEG; ∴∠DGB=∠DAB=90°; ∴BE⊥DF. |
题目简介
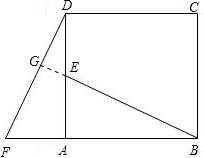
如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=12AB,已知△ABE≌△ADF.(1)在图中可以通过平移、翻折、旋转中哪一种方法,使△ABE变到△ADF的位置;(2)线段BE与
题目详情
(1)在图中可以通过平移、翻折、旋转中哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.