请阅读下列材料：问题：将一副直角三角板（Rt△ABC和Rt△DEF）如图1所示的方式摆放．其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥B

题目简介

题目详情

请阅读下列材料：
问题：将一副直角三角板（Rt△ABC和Rt△DEF）如图1所示的方式摆放．其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N．探究线段OM与ON的数量关系．
小聪同学的思路是：连接OC，构造全等三角形，经过推理使问题得到解决．

360优课网

请你参考小聪同学的思路，探究并解决下列问题：
（1）直接写出上面问题中线段OM与ON的数量关系；
（2）将这幅直角三角板如图2所示的方式摆放．使点D落在BA的延长线上，DE∥AC，FD的延长线与CA的延长线交于点M，BC的延长线与DE交于点N．点O是AB的中点．连接ON、OM、MN．请你判断线段OM与ON的数量关系和位置关系，并证明你的结论．

题型：解答题难度：中档来源：不详

答案

（1）OM=ON；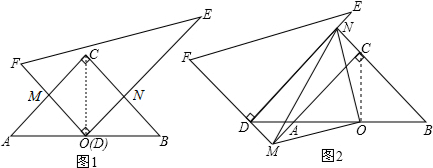

（2）OM=ON，OM⊥ON，
证明：连接OC．
∵AC=BC，O是AB中点，∠ACB=90°，
∴OA=OB，CO⊥AB，∠ACO=∠BCO=45°，
∴∠CAB=∠CBA=45°，
∴∠CAB=∠ACO，∠B=∠BCO，
∴OC=OA=OB，
∴∠MAO=∠NCO=135°，
∵DE∥MC，∠FDE=90°，
∴∠DMC=∠FDE=90°，∠DNM=∠NMC．
∵∠CAB=∠DAM=45°，
∴∠MDA=∠DAM=45°．
∴DM=AM，
∵DE∥MC，
∴∠CMN=∠DNM，
∵在△DMN和△CNM中

∠NDM=∠NCM

∠DNM=∠CMN

MN=MN

，
∴△DMN≌△CNM（AAS），
∴CN=DM=AM，
∴DM=NC．
即∠CNO=∠ODM=45°，CN=DM，∠NCO=∠MAO=135°，
∵OC=OA，
∴△AMO≌△CNO（SAS），
∴OM=ON，∠MOA=∠NOC，
∵∠NOC+∠NOA=90°，
∴∠MOA+∠NOA=90°．
∴OM⊥ON．

上一篇 : 如图：在Rt△ABC中，∠C=90°，∠A=3
下一篇 : 等腰直角三角形ABC中，AB=AC，则AB

请阅读下列材料：问题：将一副直角三角板（Rt△ABC和Rt△DEF）如图1所示的方式摆放．其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥B

题目简介

题目详情

答案

更多内容推荐