| (1)证明:∵DB⊥BC,CF⊥AE, ∴∠DCB+∠D=∠DCB+∠AEC=90°. ∴∠D=∠AEC. 又∵∠DBC=∠ECA=90°, 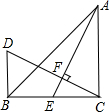 且BC=CA, ∴△DBC≌△ECA(AAS). ∴AE=CD. (2)由(1)得AE=CD,AC=BC, ∴△CDB≌△AEC(HL), ∴BD=CE, ∵AE是BC边上的中线, ∴BD=EC=
∴BD=6cm. |
| (1)证明:∵DB⊥BC,CF⊥AE, ∴∠DCB+∠D=∠DCB+∠AEC=90°. ∴∠D=∠AEC. 又∵∠DBC=∠ECA=90°,  且BC=CA, ∴△DBC≌△ECA(AAS). ∴AE=CD. (2)由(1)得AE=CD,AC=BC, ∴△CDB≌△AEC(HL), ∴BD=CE, ∵AE是BC边上的中线, ∴BD=EC=
∴BD=6cm. |
题目简介
如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(1)求证:AE=CD;(2)若AC=12cm,求BD的长.-数学
题目详情
F的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.