 (1)成立. 理由:∵点O是BC的中点 ∴BO=CO=
∵∠BAC=90° ∴AO=
∴OA=OB=OC; (2)成立. 理由:∵O是BC的中点 ∴AO是Rt△ABC的BC边上的中线 又∵AB=AC, ∴AO⊥BC,AO平分∠BAC, ∴∠B=∠OAN=45°,AO=BO, ∵在△OAN和△OBM中,
∴△OAN≌△OBM(SAS); (3)△OMN是等腰直角三角形; 理由:∵O是BC的中点 ∴AO是Rt△ABC的BC边上的中线 又∵AB=AC, ∴AO⊥BC,AO平分∠BAC, ∴∠B=∠OAN=45°,AO=BO, ∵AN=BM, ∴AN=BM, ∵在△OAN和△OBM中,
∴△OAN≌△OBM(SAS); ∴OM=ON,∠AOM=CON, ∴∠MON=∠MOC+∠CON=∠MOC+∠AOM=∠AOC=90°, ∴△OMN是等腰直角三角形. |
题目简介
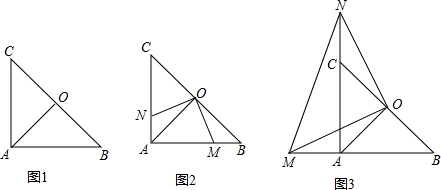
如图1,在Rt△ABC中,AB=AC,∠BAC=90°,点O是BC的中点,连接OA.(1)OA=OB=OC成立吗?请说明理由.(2)如图2,若点M,N分别在线段AB,AC上移动,在移动中始终保持AN=
题目详情
(1)OA=OB=OC成立吗?请说明理由.
(2)如图2,若点M,N分别在线段AB,AC上移动,在移动中始终保持AN=BM,△OAN≌△OBM成立吗?,并说明理由.
(3)如图3,若点M,N分别在线段BA.AC的延长线上移动,在移动中始终保持AN=BM,请判断△OMN的形状,并说明理由.